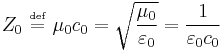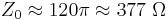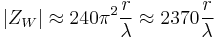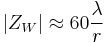Near and far field
The near field (or near-field) and far field (or far-field) and the transition zone are regions of the electromagnetic radiation field that emanates from a transmitting antenna, or as a result of radiation scattering off an object. Certain behavior characteristics of electromagnetic fields dominate at a given distance from the antenna or scattering object, while different behavior can dominate at another distance. Defined boundary regions categorize these behavior characteristics. For antennas shorter than half of the wavelength of the radiation they emit, these regional boundaries are measured in terms of a ratio of the distance from the radiating source to the wavelength of the radiation. For antennas physically larger than a half-wavelength of the radiation they emit, the antenna dimension factor must be taken into account also, and this extends the near-field region.
The "far-field" extends outward to infinity, beginning about two wavelengths distance from an electromagnetically "short" antenna. A "short" antenna is defined in this context as one that is shorter than half the wavelength of the radiation it emits (see rules for longer antennas, below). The far-field is the region in which the field acts as "normal" electromagnetic radiation. The power of this radiation decreases as the square of distance from the antenna, and absorption of the radiation has no effect on the transmitter. By contrast, the "near-field", which is inside about one wavelength distance from the antenna, is a region in which there are strong inductive and capacitative effects from the currents and charges in the antenna that cause electromagnetic components that do not behave like far-field radiation. These effects decrease in power far more quickly with distance than do the far-field radiation effects. Also, in the part of the near-field closest to the antenna (called the "reactive near-field", see below), absorption of electromagnetic power in the region by a second device has effects that feed-back to the transmitter, increasing the load on the transmitter that feeds the antenna by decreasing the antenna impedance that the transmitter "sees". Thus, the transmitter can sense that power has been absorbed from the closest near-field zone, but if this power is not absorbed by another antenna, the transmitter does not supply as much power to the antenna, nor does it draw as much from its own power supply. Finally, the "transition zone" between these near and far field regions, extending over the distance from one to two wavelengths from the antenna, is the intermediate region in which both near-field and far-field effects are important. In this region, near-field behavior dies out and ceases to be important, leaving far-field effects as dominant interactions. The image above-right shows these regions and boundaries.
Such regions categorize field behaviors that vary, even within the region of interest. Thus, the boundaries for these regions are approximate "rules of thumb", as there are no precise cutoffs between them (all behavioral changes with distance are smooth changes). Even when precise boundaries can be defined in some cases, based primarily on antenna type and antenna size, experts may differ in their use of nomenclature to describe the regions.
For antennas that have a characteristic physical length longer than one-half wavelength of the radiation they emit, and for focused or "dish" antennas of diameter longer than one half wavelength of the radiation they emit, the near and far-field distances cannot be in terms of simple radiation wavelength, but must be qualified in terms of the factor 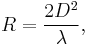 where R is the distance from the antenna, D is the antenna diameter or length, and λ is the wavelength of the radiation. When this distance R is smaller than two wavelengths of the radiation, the region inside this radius is considered near-field, but when R is longer than two wavelengths, this region is considered the antenna far-field. The behaviors in these regions are the same as described above for electromagnetically "short" antennas. This behavior of considerably extends the near-field effects of focused antennas, and antennas that emanate high-frequency radiation.
where R is the distance from the antenna, D is the antenna diameter or length, and λ is the wavelength of the radiation. When this distance R is smaller than two wavelengths of the radiation, the region inside this radius is considered near-field, but when R is longer than two wavelengths, this region is considered the antenna far-field. The behaviors in these regions are the same as described above for electromagnetically "short" antennas. This behavior of considerably extends the near-field effects of focused antennas, and antennas that emanate high-frequency radiation.
Contents |
Propagation characteristics
Any electromagnetic radiation consists of an electric field component E and a magnetic field component H. In the far-field, the relationship between the electric field component E and the magnetic component H is that characteristic of any freely propagating wave, where (in units where c = 1) E is equal to H at any point in space. By contrast, in the near-field, the relationship between E and H becomes very complex. Also, unlike the far-field where electromagnetic waves are usually characterized by a single polarization type (horizontal, vertical, circular, or elliptical), all four polarization types can be present in the near-field.[1]
The near-field itself is further divided into the reactive near-field and the radiative near-field. The "reactive" and "radiative" near-field designations are also a function of wavelength (or distance). However, these boundary regions are a fraction of one wavelength within the near-field. The outer boundary of the reactive near-field region is commonly considered to be a distance of 1/2π times the wavelength (λ/2π or 0.159 x λ) from the antenna surface. The radiative near-field (also called the "Fresnel region") covers the remainder of the near-field region, from λ/2π out to λ (one full wavelength).[1]
Reactive near-field, or the nearest part of the near-field
In the reactive near-field (very close to the antenna), the relationship between the strengths of the E and H fields is often too complex to predict. Either field component (E or H) may dominate at one point, and the opposite relationship dominate at a point only a short distance away. This makes finding the true power density in this region problematic. This is because to calculate power, not only E and H both have to be measured but the phase relationship between E and H must also be known.[1]
In this reactive region, not only is an electromagnetic wave being radiated outward into far-space but there is a "reactive" component to the electromagnetic field, meaning that the nature of the field around the antenna is sensitive to, and reacts to, EM absorption in this region (this is not true for absorption far from the antenna, which has no effect on the transmitter or antenna near-field).
Very close to the antenna, in the reactive region, energy of a certain amount, if not absorbed by a receiver, is held back and is stored very near the antenna surface. This energy is carried back and forth from the antenna to the reactive near-field by electromagnetic radiation of the type that slowly changes electrostatic and magnetostatic effects. For example, current flowing in the antenna creates a purely magnetic component in the near-field, which then collapses as the antenna current begins to reverse, causing transfer of the field's magnetic energy back to electrons in the antenna as the changing magnetic field causes a self-inductive effect on the antenna that generated it. This returns energy to the antenna in a regenerative way, so that it is not lost. A similar process happens as electric charge builds up in one section of the antenna under the pressure of the signal voltage, and causes a local electric field around that section of antenna, due to the antenna's self-capacitance. When the signal reverses so that charge is allowed to flow away from this region again, the built-up electric field assists in pushing electrons back in the new direction of their flow, as with the discharge of any unipolar capacitor. This again transfers energy back to the antenna current.
Because of this energy storage and return effect, if either of the inductive or electrostatic effects in the reactive near-field transfers energy to electrons in a different (nearby) conductor, this energy is lost to the primary antenna, and thus an extra drain is seen on the transmitter circuit, resulting from the reactive near-field energy that is not returned.
The reactive component of the near-field can give ambiguous or undetermined results when attempting measurements in this region. In other regions, the power density is inversely proportional to the square of the distance from the antenna. In the vicinity very close to the antenna, however, the energy level can rise dramatically with only a small decrease in distance toward the antenna. In the short term, and the long term, this energy can adversely affect both humans and measurement equipment because of the high powers involved.[1]
Radiative near-field (Fresnel region), or farthest part of the near-field
The radiative near-field (sometimes called the Fresnel region) does not contain reactive field components from the source antenna, since it is so far from the antenna that back-coupling of the fields becomes out-of-phase with the antenna signal, and thus cannot efficiently store and replace inductive or capacitative energy from antenna currents or charges. The energy in the radiative near-field is thus all radiant energy, although its mixture of magnetic and electric components are still different from the far-field. Further out into the radiative near-field (one half wavelength to 1 wavelength from the source), the E and H field relationship is more predictable, but the E to H relationship is still complex. However, since the radiative near-field is still part of the near-field, there is potential for unanticipated (or adverse) conditions.
For example, metal objects such as steel beams can act as antennas by inductively receiving and then "re-radiating" some of the energy in the radiative near-field, forming a new radiating surface to consider. Depending on antenna characteristics and frequencies, such coupling may be far more efficient than simple antenna reception in the yet-more-distant far-field, so far more power may be transferred to the secondary "antenna" in this region than would be the case with a more distant antenna. When a secondary radiating antenna surface is thus activated, it then creates its own near-field regions, but the same conditions apply to them.[1]
Radiation zone, including radiating far-field
The near-field and far-field of an antenna or other isolated source of electromagnetic radiation are regions around the source. The boundary between the two regions is only vaguely defined, and depends on the dominant wavelength (λ) emitted by the source. In broad terms, for an electromagnetically short antenna, the near-field is the region within a radius r << λ, while the far field is the region for which r >> λ. The two regions are defined simply for mathematical convenience, enabling certain simplifying approximations. These regions are sometimes also called the "near-zone" and "far-zone". The latter is also frequently referred to as the "radiation zone", or "free space".
A more precise definition is given by the propagation properties. If the distance separating the transmitting and receiving antennas is larger than 2D2/λ, where D is the largest dimension of the source of the radiation, then it is a far field measurement (Fraunhofer diffraction) and if the measuring distance is less 2D2/λ, it is a near-field measurement (Fresnel diffraction).
The radiation zone is important because far-fields in general fall off in amplitude by 1/r. This means that the total energy per unit area at a distance r is proportional to 1/r2. The area of the sphere is proportional to r2, so the total energy passing through the sphere is constant. This means that the far-field energy actually escapes to infinite distance (it radiates).
The amplitude of other components of the electromagnetic field close to the antenna may be quite powerful, but, because of more rapid fall-off with distance than 1/r behavior, they do not radiate energy to infinite distances. Instead, their energies remain trapped in the region near the antenna, not drawing power from the transmitter unless they excite a receiver in the area close to the antenna. Thus, the near-fields only transfer energy to very nearby receivers, and, when they do, the result is felt as an extra power-draw in the transmitter. As an example of such an effect, power is transferred across space in a common transformer or metal detector by means of near-field phenomena (in this case inductive coupling), in a strictly "short-range" effect (i.e., the range within one wavelength of the signal).
Summary
If sinusoidal currents are applied to a structure of some type, electric and magnetic fields will appear in space about that structure. If those fields extend some distance into space the structure is often termed an antenna. Such an antenna can be an assemblage of conductors in space typical of radio devices or it can be an aperture with a given current distribution radiating into space as is typical of microwave or optical devices. The actual values of the fields in space about the antenna are usually quite complex and can vary with distance from the antenna in various ways.
Since in many practical applications one is interested only in effects where the distance from the antenna to the observer is very much greater than the largest dimension of the transmitting antenna, the equations describing the fields created about the antenna can be simplified by assuming a large separation and dropping all terms that provide only minor contributions to the final field. These simplified distributions have been termed the "far-field" and usually have the property that the angular distribution of energy does not change with distance, however the energy levels still vary with distance and time. Such an angular energy distribution is usually termed an antenna pattern.
Note that, by the principle of reciprocity, the pattern observed when a particular antenna is transmitting is identical to the pattern measured when the same antenna is used for reception. Typically one finds simple relations describing the antenna far field patterns, often involving trigonometric functions or at worst Fourier or Hankel transform relationships between the antenna current distributions and the observed far field patterns. While far-field simplifications are very useful in engineering calculations, this does not mean the near-field functions cannot be calculated, especially using modern computer techniques. An examination of how the near-fields form about an antenna structure can give great insight into the operations of such devices.
The near-field is remarkable for reproducing classical electromagnetic induction and electric charge effects on the EM field, which effects "die-out" with increasing distance from the antenna (with magnetic field strength proportional to the inverse-cube of the distance and electric field strength proportional to inverse-square of distance), far more rapidly than do the classical radiated EM far-field (E and B fields proportional simply to inverse-distance). Typically near-field effects are not important farther away than a few wavelengths of the antenna.
Far near-field effects also involve energy transfer effects that couple directly to receivers near the antenna, affecting the power output of the transmitter if they do couple, but not otherwise. In a sense, the near-field offers energy that is available to a receiver only if the energy is tapped, and this is sensed by the transmitter by means of answering electromagnetic near-fields emanating from the receiver. Again, this is the same principle that applies in induction coupled devices, such as a transformer, which draws more power at the primary circuit, if power is drawn from the secondary circuit. This is different with the far-field, which constantly draws the same energy from the transmitter, whether it is immediately received, or not.
Analysis
Solving Maxwell's equations for the electric and magnetic fields for a localized oscillating source, such as an antenna, surrounded by a homogeneous material (typically vacuum or air), yields fields that, far away, decay in proportion to 1/r where r is the distance from the source. These are the radiating fields, and the region where r is large enough for these fields to dominate is the far field.
In general, the fields of a source in a homogeneous isotropic medium can be written as a multipole expansion.[2] The terms in this expansion are spherical harmonics (which give the angular dependence) multiplied by spherical Bessel functions (which give the radial dependence). For large r, the spherical Bessel functions decay as 1/r, giving the radiated field above. As one gets closer and closer to the source (smaller r), approaching the near-field, other powers of r become significant.
The next term that becomes significant is proportional to 1/r2 and is sometimes called the induction term.[3][4] It can be thought of as the primarily magnetic energy stored in the field, and returned to the antenna in every half-cycle, through self-induction. For even smaller r, terms proportional to 1/r3 become significant; this is sometimes called the electrostatic field term and can be thought of as stemming from the electrical charge in the antenna element.
Very close to the source, the multipole expansion is less useful (too many terms are required for an accurate description of the fields). Rather, in the near-field, it is sometimes useful to express the contributions as a sum of radiating fields combined with evanescent fields, where the latter are exponentially decaying with r. And in the source itself, or as soon as one enters a region of inhomogeneous materials, the multipole expansion is no longer valid and the full solution of Maxwell's equations is generally required.
Near-field
The term "near-field region" (also known as the "near-field" or "near-zone") has the following meanings with respect to different telecommunications technologies:
- The close-in region of an antenna where the angular field distribution is dependent upon the distance from the antenna.
- In the study of diffraction and antenna design, the near-field is that part of the radiated field that is below distances shorter than the Fresnel parameter[5] S = D2/(4λ) from the source of the diffracting edge or antenna of longitude or diameter D.
- In optical fiber communications, the region close to a source or aperture.
The diffraction pattern in the near-field typically differs significantly from that observed at infinity and varies with distance from the source.
Far-field
The "far-field region" is the region outside the near-field region, where the angular field distribution is in essence independent of distance from the source. In the far-field, the shape of the antenna pattern is independent of distance. If the source has a maximum overall dimension D (aperture width) that is large compared to the wavelength λ, the far-field region is commonly taken to exist at distances from the source, greater than Fresnel parameter S = D2/(4λ), S > 1.
For a beam focused at infinity, the far-field region is sometimes referred to as the "Fraunhofer region". Other synonyms are "far-field", "far-zone", and "radiation field".
Impedance
The electromagnetic field in the far-field region of an antenna is independent of the type of field radiated by the antenna. The wave impedance is the ratio of the strength of the electric and magnetic fields, which in the far-field are in phase with each other. Thus, the far-field "impedance of free space" is resistive and is given by:
Using the usual approximation for the speed of light in free space c0 = 3 × 108 m/s gives the frequently used expression:
The electromagnetic field in the near-field region of an electrically small coil antenna is predominantly magnetic. For small values of r/λ, the wave impedance of an inductor is low and inductive, at short range being asymptotic to:
The electromagnetic field in the near-field region of an electrically short rod antenna is predominantly electric. For small values of r/λ, the wave impedance is high and capacitive, at short range being asymptotic to:
In both cases, the wave impedance converges on that of free space as the range approaches the far field.[6]
Quantum field theory view
In the quantum view of electromagnetic interactions, far-field effects are manifestations of real photons, whereas near-field effects are due to a mixture of real and virtual photons. Virtual photons composing near-field fluctuations and signals, have effects that are of far shorter range than those of real photons.
See also
- Local effects
- Fresnel diffraction for more on the near-field
- Fraunhofer diffraction for more on the far field
- Near field communication for more on near field communication technology
- Resonant inductive coupling for magnetic device applications
- Wireless energy transfer for some power transfer applications
- MRI scanner A machine that transfers signals to and from the patient by near field magnetic effects at RF frequencies
- Other
- Antenna measurement covers Far-Field Ranges (FF) and Near-Field Ranges (NF), separated by the Fraunhofer distance.
- Ground waves is a mode of propagation.
- Sky waves is a mode of propagation.
- Inverse-square law
References
- ^ a b c d e Occupational Safety and Health Administration, Cincinnati Technical Center (May 20, 1990). "Electromagnetic Radiation and How It Affects Your Instruments. Near field vs. Far field." (Department of Labor - Public Domain content. Most of the content referenced by this work in this article is copied from a public domain document. In addition, this paper has provided references.). U.S. Dept of Labor. http://www.osha.gov/SLTC/radiofrequencyradiation/electromagnetic_fieldmemo/electromagnetic.html#section_6. Retrieved 2010-05-09.
- ^ John David Jackson, Classical Electrodynamics, 3rd edition (Wiley: New York, 1998)
- ^ Johansson, J. and Lundgren, U., EMC of Telecommunication Lines
- ^ Capps, C., Near field or far field?, EDN, 16 August 2001
- ^ Acoustic waves: devices, imaging, and analog signal processing, G.Kino, Ed. Prentice Hall (2000) Ch.3 p.165
- ^ Near and Far Fields - From Statics to Radiation
- This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).
- This article incorporates public domain material from websites or documents of the United States Government. Occupational Safety and Health Administration
Patents
- George F. Leydorf, U.S. Patent 3,278,937, Antenna near field coupling system. 1966.
- Grossi et al., U.S. Patent 3,445,844, Trapped Electromagnetic Radiation Communication System. 1969.
- U.S. Patent 3,461,453, Reducing-Noise With Dual-Mode Antenna. 1969.
- Coffin et al., U.S. Patent 3,662,389, Determination of Far Field Antenna Patterns Using Fresnel Probe Measurements. 1972.
- Hansen et al., U.S. Patent 3,879,733, Method and Apparatus for Determining Near-Field Antenna Patterns. 1975
- Wolff et al.,U.S. Patent 5,459,405, Method and apparatus for sensing proximity of an object using near-field effects